leetcode

首先想到让每个cell保存相邻cell信息, 然后利用回调来更新, 代码如下

数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。
有时候胜出者并非有最好的算法，而是有更多的数据。

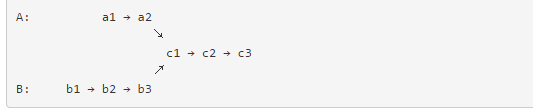
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)

提纲

• 0 Review

• 1 different variations of MDPs
  • 1.1 State-Action Rewards
  • 1.2 Finite Horizon MDPS

• 2 Linear Dynamical Systems
  • 2.1 Linear Quadratic Regulation
  • 2.2 Riccati Equation

手头有一个垃圾路由器，一直吃灰，闲着没事就刷了openwrt玩玩，本着物尽其用的原则，不如开个后门然后送人吧。。

开端

曾经偶然得到了某运营商的一个瘦AP，发现这玩意厉害了。百度一下，发现功率够大，能覆盖三四百米，轻松穿两堵墙。于是根据用户手册，把电脑静态地址改成192.168.0.1，进入web系统。点点鼠标，顺利切换到胖AP模式，完全变身家用路由器了。开一个热点果然效果惊人，2.4G和5G双频通吃，楼下都能信号满格，好爽。然后我就把密码去了，好让邻居们一起爽爽。

第二天我就发现有点不对劲了，上nmap扫了一遍，发现这货默认开放ssh和telnet。telnet好说，web管理可以关。ssh我找了半天没找到。。

zfs是sun公司开发的下一代文件系统，使存储管理更为简单。

软件管理

Gentoo Portage

在这一节，我们会告诉大家怎样在Gentoo中安装软件、Gentoo的Portage系统是什么、Portage树是什么。这一节内容是Gentoo特有的，事实上，如果你不是一个Gentoo用户，你还是会感到愉悦，尽管不能使用。

简介

Gentoo主要是一个基于源代码的Linux发行版。这意味着不像其他操作系统，Gentoo不只是在你的文件系统里放置已经编译好的文件。而是从互联网拉取你需要的源代码、配置编译环境、生成软件。

简介对于一个简单的二分类问题，利用输入向量x预测y为正样本或负样本，学习参数为频率学派贝叶斯学派判别模型生成模型 就分类任务而言, 直接学习(直接学习输入空间到输出标签的映射), 就是判别模型. 而生成模型试图为输入建模, 训练完成后, 运用贝叶斯规则乘上先验转化为后验使用. 频率学派通过给 ...

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

var o = (function() { var person = { name: 'Vincent', age: 24 }; return { run: function(k) { return person[k]; } } })(); // TODO 在不改变上面代码的基础上，并且在只知道 person 是一个对象的基础上 // 只能在本段注释后面继续写代码，最终通过 o 打印出 person ，对于上文中的 person 即 `Object {name: "Vincent", age: 24}` // 例如 o.someThing = 1; cosnole.log(o.run('someThing')); // 在考虑到 person 为未知对象的基础上，尽可能写出更加完善的代码。 // 最终，如果不能完成该题，请尽可能的记录下来你思考的过程。